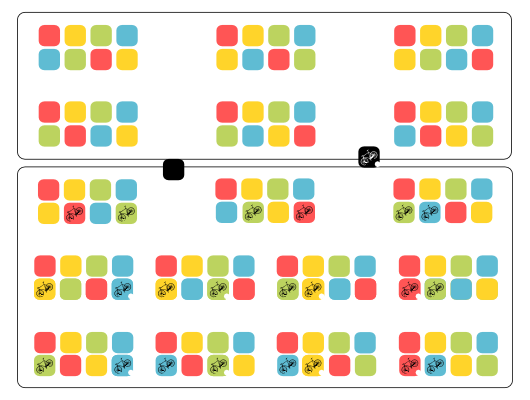
Digital Sketch: Permutations and Cycles
This is a digital sketch inspired by the equality:
$$ C(n,k) = C(n-1,k-1) + C(n-1,k) (n-1), $$
where $C(n,k)$ denotes the number of permutations of, say, $[n]$ with $k$ cycles. The equality is nearly self-explanatory — you simply knock off one of the elements (let’s do away with $n$) and stare at permutations of $[n-1]$.
In particular, look at permutations of $[n-1]$ that have $(k-1)$ cycles: such permutations can be extended to permutations of $[n]$ with $k$ cycles by simply adding the element $n$ and letting the permutation take $n$ to itself. On the other hand, for all permutations that have $k$ cycles, we might “insert”, so to speak, the element $n$ into one of the existing cycles. A moments reflection tells us that this can be done in one of $(n-1)$ ways, for there are as many slots for insertion — when considered in total.
These observations written out amount to the identity we had.