Masters Thesis
On the Infeasibility of Polynomial Kernelization
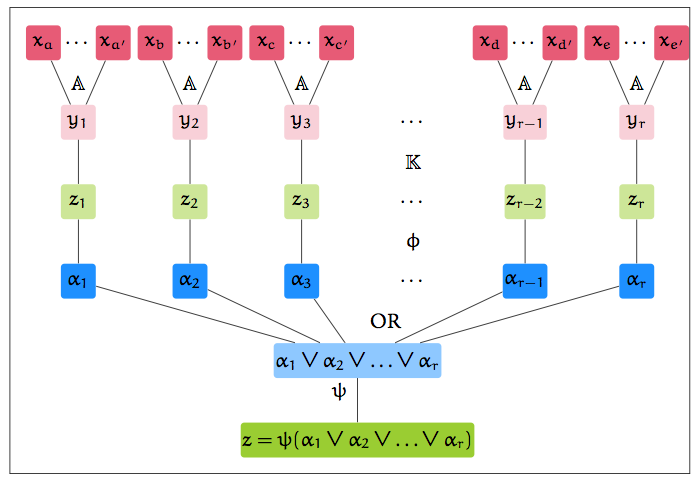
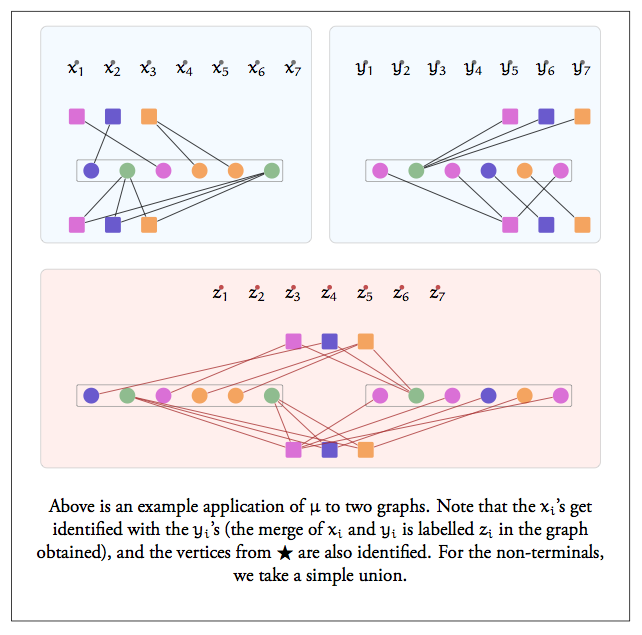
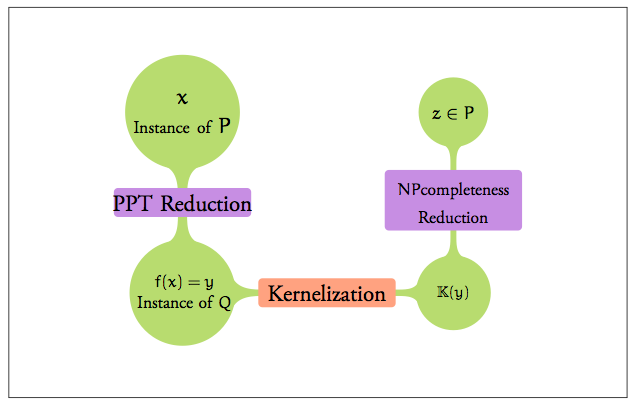
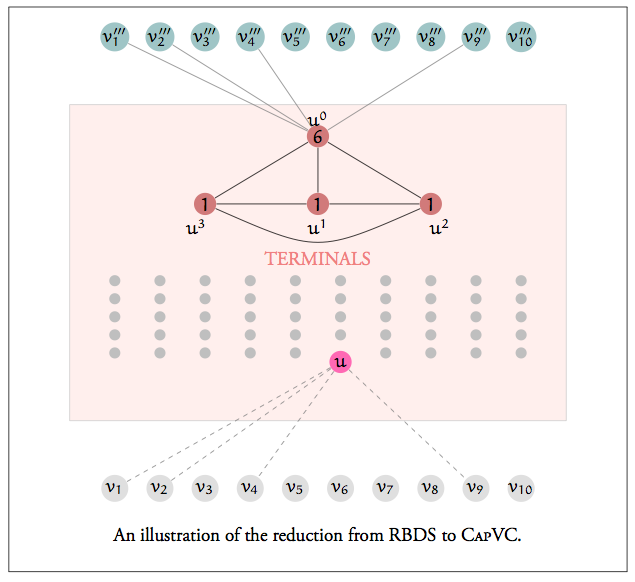
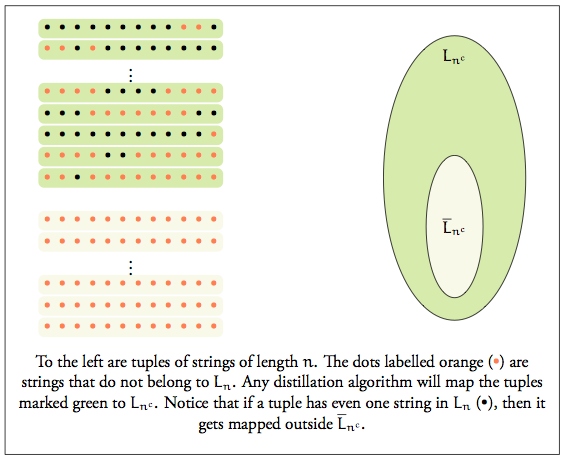
This thesis is a leisurely survey of lower-bound techniques in the context of kernelization (polynomial kernels in particular - see this survey for a compressed version), which saw a number of exciting breakthroughs during the time that the thesis was written, and continues to enjoy very active development.
Remark: Methods in showing kernel lower bounds have advanced considerably. New developments include — but are not limited to — the technique of cross-composition and the framework for demonstrating finer lower bounds. Also, the AND Conjecture, stated as one of the major open problems in the area, has since been resolved. Here’s a blog post about the result. Techniques for “coping” with the hardness of polynomial kernelization are fast evolving as well, and one of the relatively recent paradigms in this direction is Lossy Kernelization, which is a robust notion of “approximate” kernels.
Advisor: Prof. Venkatesh Raman